Использование метода моделирования в начальной школе на уроках математике

Использование метода моделирования в начальной школе на уроках математике

Аннотация. В статье рассматриваются модели (рисунок, схема, графическая модель, схематический чертёж, таблица), которые можно использовать учителю начальных классов на уроке математике.

Государственные образовательные стандарты (ФГОС НОО) ставят овладение УУД во главу, среди которых важную роль играет моделирование (познавательные УУД). Освоение данного действия позволит учащимся не только самостоятельно усваивать новые знания и умения, но и полноценно формировать мотивацию к обучению и умение свободно ориентироваться в предметных областях.
В настоящее время перед педагогами стоит проблема в необходимости выявления педагогических условий и поиске путей эффективного овладения моделированием на уроках математики.

Метод моделирования, разработан Д.Б. Элькониным, Л.А. Венгером, Н.А. Ветлугиной, Н.Н. Поддьяковым, заключается в том, что мышление ребенка развивают с помощью специальных схем, моделей, которые в наглядной и доступной для него форме воспроизводят скрытые свойства и связи того или иного объекта.

В основе метода моделирования лежит принцип замещения: реальный предмет ребёнок замещает другим предметом, его изображением, каким-либо условным знаком. При этом учитывается основное назначение моделей – облегчить ребёнку познание, открыть доступ к скрытым, непосредственно не воспринимаемым свойствам, качествам вещей, их связям. Эти скрытые свойства связи весьма существенны для познаваемого объекта. В результате знания ребенка поднимаются на более высокий уровень обобщения, приближаются к понятиям.

В учебном процессе бывают случаи, когда просто необходимо моделирование:

- класс встречается с новым видом задач;

- педагогу нужно проконтролировать осознанность решения задач учащимися;

- «слабые» ученики не могут обойтись без модели, и им разрешается сделать модель наиболее понятного для них вида.

Поскольку уровень интеллектуального развития у детей разный, то нельзя, не учитывая индивидуальных особенностей ребёнка, научить его решать по шаблону любую задачу. Ученикам м различным уровнем развития требуется различные приёмы работы с задачей, поэтому на уроках математики я учу детей построению нескольких видов моделей одной и той же текстовой задаче. Это требуется для того, чтобы учащиеся не оказались в ситуации неуспеха, а чувствовали себя способными решить любую задачу.

Виды моделей:

1.       Рисунок изображает реальные предметы, о которых говорится в задаче, или условные предметы в виде геометрических фигур.

В целях формирования осознанного подхода к составлению и применению моделей в виде рисунка в учебнике к задаче даю следующие задания:

- какой рисунок подходит к данной задаче?                                 
- составь по другому рисунку задачу и реши её.

Эти задания способствует формированию навыка составления и анализа моделей.

2.       Схема является наиболее предпочтительной моделью при решении задач по ряду причин:

- может быть использована при решении задач со сколь угодно большими числами;

- может применяться при решении задач с буквами;

- позволяет подняться на достаточно высокую ступень абстрактности:

3. Графическая модель  - схема сюжетной задачи помогает понять учащимся абстрактные отношения, заданные в условии задачи, в конкретной пространственной форме. Схема является обобщением, позволяющим выйти за пределы данной задачи и получить обобщающий способ для решения любых задач данной структуры.

Задача.
                У Даши было 3 яблока, а у Паши на 1 яблоко меньше. Сколько яблок у Паши?

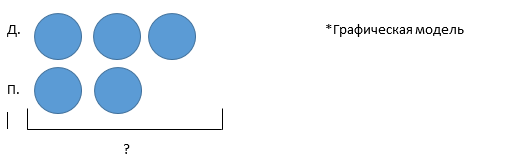
Решение:

1)      3-1= 2 (я)
       Ответ: 2 яблока у Паши.

К приёмам моделирования относятся также схемы (иллюстрация, отражающая суть построения предмета). Схемы можно применять на уроках математики при решении задач с буквами, с большими числовыми значениями, показывая тем самым характер процесса, повествующего условия задачи. Схемы – это обобщающий способ для решения задач. Применение схем и чертежей на уроках математики делает учебный материал более доступным для младших школьников.

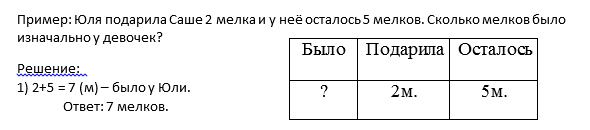
Наиболее распространённым способом моделирования является таблица. Это текстовая или числовая информация, представленная в определенном порядке. Учащиеся могут заполнять таблицы, как на уроке, так и дома при выполнении домашнего задания.

При этом учитель совместно с классом может провести обсуждение заполненного материала. Следует отметить, то существует несколько видов таблиц. Один из них сравнительная таблица, которая способствует более качественному выполнению домашнего задания, так как в ней предоставлена основная информация на урок. В то же время сравнительные таблицы можно применять как при разборе новой темы, так и на этапе закрепления знаний.

Работа с моделями позволяет учителю стимулировать самостоятельную деятельность учащихся. Так дети сами выбирают и строят модели, а затем работают с ними. Например, при решении ситуативных задач обучающиеся могут представить модель какой-либо реальной ситуации описанной в условиях задачи, затем изучив её прийти к решению.

Таким образом, применение различных способов моделирования на уроках математики способствует развитию логического мышления учащихся, при этом раскрываются их творческие способности.
Дети учатся не только анализу информации, но и способам её замены на графические символы, что позволяет лучшему запоминанию материала.

Моделирование позволяет  значительно экономить время на выполнение различных заданий. Оно даёт возможность учителю сформировать у учащихся умение работать с информацией на уроках математики в начальной школе.